Theoretical Background for Deterministic Volatility Models

Term structure of interest rates

Derman and Kani (1997) provide an analogy of DVF and IVT with models of the Term Structure of interest rates.  Heath, Jarrow, and Morton (1990, henceforth HJM) develop a model for interest rates where the inputs are forward interest rates, f_t,T as follows 

                                                            (3)

This is the differential form of the forward rate curve given an initial forward rate f_0,T for each maturity T.  m_t,T and s_t,T are the mean and volatility of the forward curve and can be functions of the brownian motion, dz, or past forward levels, f_i,T for i<T.  Given that an initial forward curve, f_0,T, is established with all traded bond prices and with the assumption that the forward curve is static as time passes.  With the term structure models, the term structure (bond prices) is specified and the forward rates extracted.  The forward rates are risk adjusted expectations of future instantaneous short rate defined as .  Duffie (1996) and Derman and Kani (1997) show that the price of zero coupon bonds are described by the deterministic backward equation, given the HJM framework as

,

where f_t,T is the for rate for each maturity as T evolves, B_t,T is the price of the zero coupon bond defined as .  Or conversely, the forward equation

.

The future evolutions of all bonds across all maturities are dependent upon this initial forward curve.  The assumptions about the volatility process provide solutions to the differential equation presented above for the interest rate models of Ho and Lee (1986), Cox, Ingersol and Ross (1985), Vasicek (1977) and others.  Baxter and Rennie (1996), Duffie (1996), and Ritchken (1996) provide detail reviews of the relationships and derivations of these models.  This framework for interest rates can be extended to volatility and is discussed in the following section.

The effective theory of volatility

The effective theory of volatility has the local volatility surface being a deterministic function of a spectrum of option prices and futures prices.  This deterministic function remains fixed (static) as time and the underlying asset change (Derman, Kani, and Chriss, 1996 and Derman and Kani, 1997).  The effective theory of volatility based on deterministic volatility functions will then incorporate a time varying or modified stochastic process and allow for inferences about the terminal distribution of the underlying asset (Derman and Kani, 94).  Based on Derman and Kani (1994 and 1997), the relationship between implied volatility and deterministic volatility functions for a futures contract can be shown.  Assume that the futures contract stochastic process is

,

where dF_t is the change in price of the futures contract, m is the mean of the process, s_F is the volatility, and dz is a random Brownian motion.  The solution to this equation is the Black-76 under the assumption of preference free or no arbitrage reasoning, geometric brownian motion (Lognormal terminal distribution), constant volatility, and constant risk free rate of interest, r. The call valuation formula is

,

where F is the futures price, K is the strike price, r is the risk-free rate of interest, Dt is the time to maturity in years, and N( * ) is the standard normal cumulative probability function.  The variables d₁ and d₂ are defined as

.

.

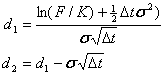This pricing model is the solution to the following stochastic differential equation or Kolmogorov backward equation

;

and the forward equation becomes

.

This relationship between the underlying asset and the volatility of this asset is easily seen from the Cox, Ross, and Rubinstein (1979) binomial approximation as shown in figure ?.  The equal spacing between the nodes of the tree at each time step exhibit the assumption of constant volatility.  The violation of the constant volatility requires adjustment of the underlying process to account for the time variation.  A modified stochastic process is required to capture the skewness and kurtosis that exists in the underlying asset.

To account for a violation of constant volatility, a simple stochastic process is

,

where s_F,t is the time varying volatility conditioned on the underlying futures price and time.  This is similar to defining a stochastic volatility model, but here the volatility process is not defined as a random process but behaves deterministically.  As stated, this is analogous to a static forward rate curve that defines an effective theory of interest rates shown by Heath, Jarrow, and Morton (1990) modeling of the term structure of interest rates  (Derman and Kani, 1997) and is a single factor continuous time model. 

The option pricing model with time varying volatility is the solution to the stochastic differential equation

,

with the forward equation being

.                                         (1)

Equation (1) can be solved for the volatility parameter for a given strike, K as

.                                               (2)

This is a local variance that is an unbiased, risk adjusted expectation of future realized variance at time T (Derman and Kani, 1997 and Fleming, 1998)[1].  The volatility s_F,t is a function of the underlying futures price, F_t, and time, t, and s_K,t is a function of the strike and time.  Fleming (1998), using Feinstein's (1989) derivation shows a similar result for near expiration at-the-money options as

These equations allow for static or non-random local volatility surface to define an effective theory of volatility that is similar to the effective interest rate theory, previously discussed, used in modeling bond price dynamics (Derman and Kani, 1997).  A relationship between strike and time to maturity is established (Dupire, 1994) if the volatility is known.

The deterministic volatility function, s_F,t or s_K,t, will allow for the skewness that is observed.  In the CIR binomial frame work, a skewed tree results with larger separation at lower index levels than at higher index levels as depicted in the following figure.  The local volatility is easily viewed as the instantaneous volatility at a particular node.  In a binomial volatility tree this is the volatility over the next transition period and is a measure of distance between the two nodes for the up or down paths in the implied tree.  The constant volatility assumption of Black-Scholes and Black-76 has equal spacing between nodes in a binomial tree, whereas a local volatility provides for the skewness in the volatility smile that is shown in figure ?.

Equation (2) shows the volatility process is equivalent to averaging out all sources of stochastic volatility.  The underlying futures price uncertainty is the only source of uncertainty that remains with the deterministic structure being a function of the underlying futures price and time.  Figure 1 shows a representation of this type of process assuming an out-of-the-money call option exists at strike K that expires at time T with current commodity level F[2].  The volatility is assume to be a linearly related to the underlying commodity and time specified as

                                                        (3)

The implied volatility represents the expected volatility and is the average volatility over the time to expiration resented by a double integration over the possible price paths of the shaded area in figure ? and defined as

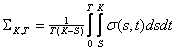
By substituting equation (3) and integrating, the expected volatility is

.

This specification shows the implied volatility is a linear function of moneyness and time with volatility increasing at one-half the commodity level and decreasing at one-half the time to expiration.

Specification of deterministic functions of volatility should have theoretical base as Ball and Roma (1994) and Taylor and Xu (1994) show.  As shown, the implied volatility is a function of time and commodity level.  Again, research in term structure models provides some insight as to the volatility processes in general.  The HJM model in equation (3) has a general specification for the volatility term as

.

This specification has the forward volatility as function of the spot volatility, s₀, the spot interest rate, and a mean reversion parameter, k.  The mean reversion model is an exponentially dampened volatility structure (Ritchken, 1996).  This general volatility structure contains several common models of forward rates based on a single factor short rate[3].  Restricting g=0, the Vasicek (1977) model volatility structure is obtained.  With k=0 and g=1/2, the Cox, Ingersol, and Ross (1986) square root volatility process is found, and if g=1, the Black Derman, and Toy (1990) model is obtained.  Another model nested within this general structure is the Ho and Lee (1986) model that requires g=0 and k=0 and this reduces to a constant term structure volatility similar to the constant volatility Black and Black-Scholes.  Forward volatility is not limited to this general specification, Amin and Ng (1997) study the linear proportional model with the volatility process described as [s₀+s₁(T-t)]f_t,T. 

Each specification of volatility in the HJM framework is a dependent function of time and forward level.  A deterministic volatility function should have the same structure.  The deterministic function developed in equation (2) remains fixed as time and the underlying asset change, resulting in lower and higher implied volatilities resulting from the price evolution (Derman and Kani, 1997 and 1999).  This type framework does not rule out a multi-factor process for volatility.  The assumption here is that the process for volatility is unknown or not understood, so a specification is not being imposed as in the stochastic volatility models (Chriss, 1997).  The process is being derived from options prices assuming that the market is efficient.