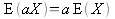
A Mathematical Review of Operations Involving Expected Values and Variances

Property 1: The expected value of the product of a constant (a) and a random variable (X) equals the product of the constant times the expected value of the random variable:

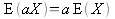
Property 2: The expected value of the two random variables (X + Y) equals the sum of their respective expected values:

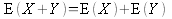
Property 3: The variance of the sum of a random variable (X) plus a constant (a) equals the variance of the random variable:

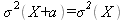
Property 4: The variance of the product of a constant (a) and a random variable (X) equals the constant squared times the variance of the random variable:

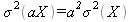
Property 5: The variance of the sum of two or more random variables (X + Y + Z) equals the sum of their respective variances plus 2 times the covariance between all different pairs of the random variables:

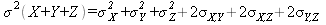
Property 6: The covariance between a pair of products of a constant and a random variable equals the product of the two constants multiplied by the covariance between the two random variables:

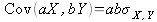
Miscellaneous Property: Assume X~LN, i.e. X is Log-Normally distributed, then the variance of the log of X is the same as the variance of the log of a constant times X. Also, the expected value of the log of X is the same as the Expected value of the log of X plus the log of a constant.

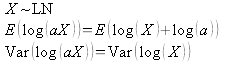
Sources:

Martin, John D.; Cox, Samuel H.; MacMinn, Richard D. The Theory of Finance: Evidence and Applications. The Dryden Press, 1988.